728x90
■ 연속확률변수와 확률분포
1. 연속확률변수
어떤 범위 안에 속하는 모든 실수의 값을 가지는 확률변수를 연속확률변수라 한다.
2. 확률밀도함수
연속확률변수 X에 대하여 α≤x≤β에서 정의된 함수 f(x)가 다음 세 가지 성질을 모두 만족시킬 때, 함수 f(x)를 확률변수 X의 확률밀도함수라고 한다.
(1) f(x)≥0
(2) y=f(x)의 그래프와 x축 및 두 직선 x=α, x=β로 둘러싸인 도형의 넓이는 1이다.
(3) P(a≤X≤b) 는 y=f(x)의 그래프와 x축 및 두 직선 x=a, x=b로 둘러싸인 도형의 넓이와 같다. (단, α≤a≤b≤β)

3. 정적분으로 연속확률변수와 확률밀도함수
(1) 확률밀도함수
연속확률변수 X가 α≤x≤β에서 모든 실수 값을 취하고, 이 범위에서 함수 f(x)가 다음 조건을 만족할 때, f(x)를 X의 확률밀도함수라 한다.
① f(x)≥0
② y=f(x)의 그래프와 x축 사이의 전체 넓이는 1이다.

③ 확률 P(a≤X≤b)는 a≤x≤b에서 y=f(x)의 그래프와 x축 사이의 넓이와 같다.
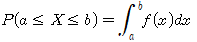
(2) 연속확률변수의 평균, 분산, 표준편차
연속확률변수 X의 확률밀도함수가 f(x) (α≤x≤β)일 때, X의 평균, 분산, 표준편차를 다음과 같 이 정의한다.
① 평균

② 분산

③ 표준편차
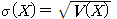
| 확률변수와 확률분포 |
반응형
'수학교과실 > 확률과 통계' 카테고리의 다른 글
| 정규분포 (0) | 2021.02.04 |
|---|---|
| 이항분포 (0) | 2021.02.04 |
| 이산확률변수의 평균과 표준편차 (0) | 2021.02.04 |
| 확률변수와 확률분포 (0) | 2021.02.04 |
| 사건의 독립과 종속 (0) | 2021.02.04 |




