■ 원에서 현과 접선의 성질
1. 접선과 현이 이루는 각
1) 접선과 현이 이루는 각 : 원의 접선과 그 접점을 지나는 현이 이루는 각의 크기는 그 각의 내부에 있는 호에 대한 원주각의 크기와 같다.

$$ \angle BAT = \angle BCA $$
2) 접선이 되기 위한 조건 : 원 O에서 $ \angle BAT = \angle BCA $이면 직선 AT는 원 O의 접선이다.
2. 원과 비례
1) 원에서의 비례 관계 : 한 원에서 두 현 AB, CD 또는 이들의 연장선이 만나는 점을 P라 하면

$$ \overline{PA} \cdot \overline{PB} = \overline{PC} \cdot \overline{PD} $$
2) 네 점이 한 원 위에 있을 조건 (비례관계)
두 선분 AB, CD 또는 이들의 연장선이 만나는 점을 P라 할 때,
$ \overline{PA} \cdot \overline{PB} = \overline{PC} \cdot \overline{PD} $
이면 네 점 A, B, C, D는 한 원 위에 있다.

3. 접선과 할선 사이의 관계
1) 접선과 할선의 관계 : 원의 외부에 있는 한 점 P에서 이 원에 그은 접선과 할선이 원과 만나는 점을 각각 T, A, B라 하면
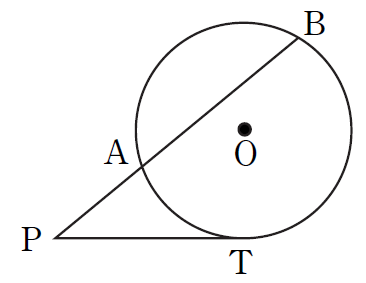
$$ \overline{PT}^2 = \overline{PA} \cdot \overline{PB} $$
2) 접선이 되기 위한 조건 : 한 직선 위에 세점 P, A, B가 있고, 이 직선 밖에 점 T가 있을 때,
$ \overline{PT}^2 = \overline{PA} \cdot \overline{PB} $
이면 $ \overline{PT}$는 세점 A, B, T를 지나는 원의 접선이다.

| 원과 직선 관계 원주각의 성질 원의 접선의 방정식 원과 직선의 위치 관계 |
'Joy Of Math > 생각넓히기' 카테고리의 다른 글
| 원주각의 성질 (0) | 2023.09.14 |
|---|---|
| 원과 직선 관계 (0) | 2023.09.13 |
| 소수란? (소수의 다양한 특성) (1) | 2022.11.18 |
| RSA암호 원리 (0) | 2022.11.11 |
| 원에 내접하는 사각형의 성질 (0) | 2021.06.18 |




