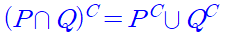728x90
■ 명제와 조건의 부정
1. 명제의 부정
명제 p에 대하여 ‘p가 아니다.’를 명제 p의 부정이라 하고, ∼p (not p)로 나타낸다.
명제 p가 참이면 ∼p는 거짓이고, p가 거짓이면 ∼p는 참이다.
또한 명제 ∼p의 부정은 p, 즉 ∼(∼p)=p이다.
예)

2. 조건의 부정
조건 p에 대하여 ‘p가 아니다.’를 조건 p의 부정이라 하고, 기호로 ∼p로 나타낸다.
또 전체집합이 U일 때, 조건 p의 진리집합을 P라 하면 그 부정 ∼p의 진리집합은
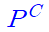
예) 전체집합이 U={x|x는 10이하의 자연수}일 때, 조건과 그 부정의 진리집합 구하기
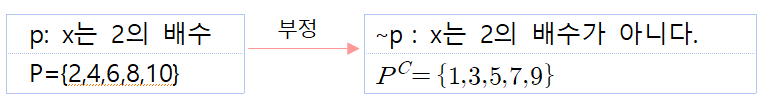
3. 조건의 부정 정리
두 조건 p, q에 대하여
| 조건 | 부정 |
| =(같다.) | ≠(같지 않다.) |
| p | ∼p |
| p 또는 q | ∼p 이고(그리고) ∼q |
| p 이고(그리고) q | ∼p 또는 ∼q |
| x<a | x≥a |
| x>a | x≤a |
| 짝수 | 홀수 |
| 음수 | 음수가 아니다. |
| x=y=z | x≠y 또는 y≠z 또는 z≠x |
| 적어도 하나는 ~이다. | 모두 ~가 아니다. |
4. 조건과 진리집합
조건 p, q의 진리집합을 각각 P, Q라 하면
| 조건 | 진리집합 |
| ∼p | |
| ∼(∼p)=p | |
| p 또는 q | P∪Q |
| p 이고 q | P∩Q |
| ∼(p 또는 q) = ∼p 이고 ∼q | |
| ∼(p 이고 q) = ∼p 또는 ∼q |
| 명제와 조건 명제 |
반응형
'수학교과실 > 수학(하)' 카테고리의 다른 글
| 명제 p → q (0) | 2021.07.23 |
|---|---|
| '모든'또는 '어떤'을 포함한 명제 (2) | 2021.07.23 |
| 명제와 조건 (0) | 2021.07.22 |
| 집합의 원소의 개수 (0) | 2021.07.21 |
| 집합의 연산법칙 (0) | 2021.07.21 |